Untersuchung dynamischer Systeme
Sie finden die Webpräsenz der Professur Mehrkörperdynamik auf www.dynamik.ovgu.de
Der Lehrstuhl beschäftigt sich mit der Untersuchung dynamischer Systeme, wobei der Dualismus zwischen numerischer Simulation und experimenteller Analyse/Verifikation eine ganzheitliche Untersuchung auch komplexer Systeme ermöglicht. In diesem Zusammenhang werden konventionelle Simulationsverfahren um zusätzliche (meist nichtlineare) Effekte erweitert und erprobte Messtechniken mit neuen Herangehensweisen kombiniert.
Abbildung des rotordynamischen Verhaltens
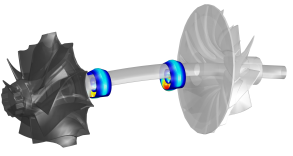
Die Simulation des dynamischen Systemverhaltens ist im Entwicklungsprozess einer Maschine ein wesentliches Element, um Aspekte wie Lagerbelastungen, Spannungen, Lebensdauer etc. vorherbestimmen zu können. Bzgl. rotordynamischer Systeme können Effekte wie Resonanz, sub- oder superharmonische Schwingungskomponenten etc. einen wesentlichen Einfluss auf diese Parameter ausüben. Aufgrund der Komplexität und häufig auftretender nichtlinearer Wechselwirkungen erfolgt die Beschreibung unter Nutzung numerischer Methoden, welche alle signifikanten Einflüsse berücksichtigen. Für die Simulationen werden sowohl klassische Mehrkörpersysteme verwendet als auch ein hybrider MKS-Rotordynamik-Ansatz eingesetzt, welcher in der inhouse entwickelten Software EMD (Homepage) integriert ist. Kontakt
 |
 |
 |
||||||
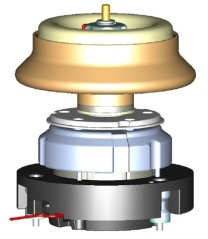
| Turbolader | Wellenstrang | Zentrifuge | ||||||
Modellierung nichtlinearer Schwingungsprozesse
Für die Simulation nichtlinearer Schwingungsprozesse ist die genaue Abbildung der Nichtlinearität wesentlich, um realitätsnahe Ergebnisse sicherzustellen. Ein Forschungsaspekt ist deshalb die Formulierung des Steifigkeits- und Dämpfungsverhaltens als Funktion der kinematischen Systemparameter, wodurch eine rückwirkungsbehaftete Beschreibung ermöglicht wird. Mit dieser Vorgehensweise können sowohl lineare Charakteristiken (konstante Federsteifigkeit und Dämpfungskonstante) als auch nichtlineare Einflüsse (Kontakt, Steifigkeit, nichtlineares Materialverhalten) ganzheitlich berücksichtigt werden. Kontakt
Experimentelle Bestimmung von Steifigkeits- und Dämpfungscharakteristiken
Für die modellgestützte Untersuchung dynamischer Systeme und ihres Verhaltens ist die Bestimmung der konkreten Systemeigenschaften (Masseneigenschaften, Steifigkeitsverhalten, Dämpfungscharakteristik) essentiell. Zum einen können auf diese Weise Validierungen numerischer Simulationen erfolgen, zum anderen ist damit auch die Ermittlung realer Kenngrößenverläufe und deren direkte Weiterverwendung möglich. Dabei kommen verschiedene Messsysteme wie Kraftsensoren, Dehnungsmessstreifen, Lasertriangulationssensoren und piezoelektrische Beschleunigungssensoren zum Einsatz. Kontakt
 |
| Messtechnische Bestimmung der Steifigkeit und Dämpfung eines Elastomerelements |
Messung von Strukturschwingungen in stehenden UND rotierenden Systemen
Während die Bestimmung der Steifigkeits- und Dämpfungscharakteristik häufig nur für Lagerelemente oder Elastomerkomponenten zielführend ist, kann alternativ auch das konkrete Schwingungsverhalten unter Betriebsbedingungen messtechnisch erfasst werden. Dazu steht dem Lehrstuhl ein 3D-Laser-Scanning Vibrometer zur Verfügung, das die gleichzeitige räumliche Aufnahme der Strukturschwingung ermöglicht. Als Erweiterung dieses Messsystems kann auch auf rotierenden Komponenten unter Nutzung eines Derotators gemessen werden, was die Untersuchung komplexer Anregungsmechanismen erlaubt. Der Laserstrahl wird über eine rotierende Optik auf das zu messende Objekt übertragen und ermöglicht so die Verfolgung körperfester Punkte auf dem Objekt. Kontakt
 |
| Bestimmung der Strukturschwingungen einer Luftschraube im rotierenden System |
Diagnose von Wälzlagerschäden
Neben Gleitlagern sind Wälzlager die am häufigsten eingesetzten Lagerelemente und stellen ein sowohl für die Lebensdauer als auch für die Akustik wesentliches Konstruktionselement dar. Infolge von Belastungen entstehen Schadstellen (Pitting oder False Brinelling) des Lagers, die zu charakteristischen Schwingungsphänomenen führen, welche aus Monitoring Signalen unter Nutzung geeigneter Filter detektiert werden. Anschließend kann modellgestützt die Position und die konkrete Fehlerart festgestellt werden, was zu einer Maximierung von Wartungsintervallen und Verringerung von Ausfallzeiten führt. Kontakt
 |
 |
|||
| Wälzlagervarianten (Quelle: Goreczka, S. Adaptives Verfahren für die Zustandsüberwachung von Wälzlagern bei unbekannten Schädigungen und unter variablen Betriebsbedingungen. Dissertation, 2013.) |
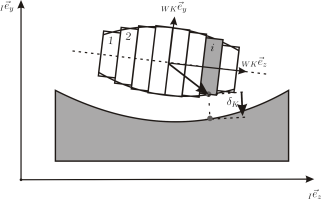
Scheibenmodell für die Kontakterkennung in Wälzlagern (Quelle: Daniel, C. Simulation von gleit- und wälzgelagerten Systemen auf Basis eines Mehrkörpersystems für rotordynamische Anwendungen. Dissertation, 2013.) |
|||
